【苦手でも解ける】中１分配法則とマイナスの計算をわかりやすく解説！

あなたは分配法則の問題が解けずに
困っていませんか？



中学１年生で習う
『分配法則』ですが、

a、ｂ、c や
x（エックス）、 y（ワイ）といった

『文字』が入ってくることによって
複雑になってきますよね。

そこにマイナスが入ってくると
さらにあたふた💦



わたしはこれまで
多くの中学生に数学を教えてきたのですが、

中学３年生になっても
分配法則で困っている生徒を

何度も見たことがあります。



分配法則は
数学を習っているとよく見かけるので、

今後のためにも習いたてほやほやのうちに

解けるようになりたいですよね♪



今回、分配法則について

特に『分かりやすい！』
『こんな簡単なんだね！』

と言ってもらえた教え方について
説明していきます。



わたしは、特に数学の基本について

教えることが多く、

たくさんの工夫をしながら

ひとりひとりに合わせながら教えてきました。



この記事を読むことで

分配法則のことを
理解してもらえるのはもちろん、

『理解しなくても答えにたどり着ける』

そんな魔法の解き方も
分かるようになりますよ！




まずは、分配法則とその公式の説明をして、

そのあとに例題や問題を解きながら

理解を深めていきましょう。



目標は分配法則の公式を覚えるだけで
問題を解けるようになること！！



この記事をよんで、

分配法則の問題を解けるようになった
あなたのテストの点数、
そして成績はぐぐっと上がりますよ♪

中１で習う分配法則を簡単に説明！

分配法則とは

分配法則は

( a + b ) × c　や　a × (b + c )　のような

かっこ『（）』が入った問題を
解くときに使います。



これからお話しする
分配法則を使うことによって

かっこ『（）』を式から消すことができるようになります。



つまり、



分配法則は
計算をして、かっこ『（）』を消したいときに使う！



かっこ『（）』を消すために

数字を『分けて』『配って』いるんですね。
（だからこそ分配法則…。ふむ！）

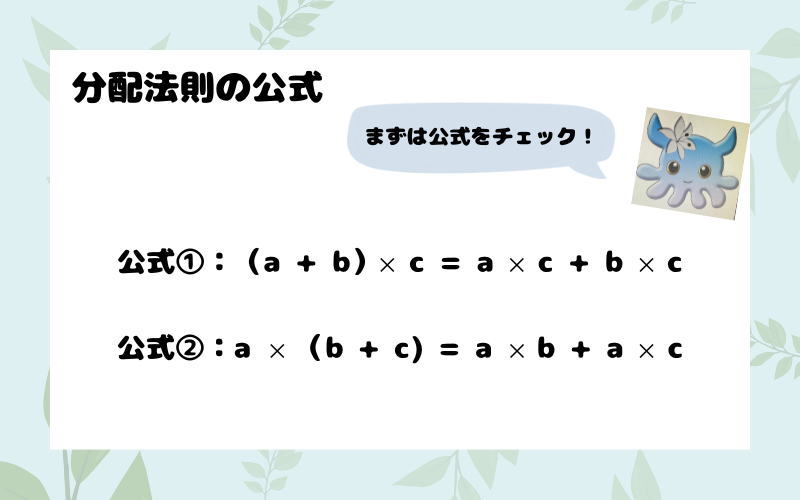
分配法則の公式について

文字を使った分配法則の公式は

次のようになっています.

そう思ったあなたのために、

実際に公式の内容を確認していきます。



公式①で考えていきます。



『　( a + b ) × c　』 と　

『 a × c + a × c 』の両方に

a = 1、b = 2、c = 3 を代入して、

同じ答えになれば問題ないのです！



それではさっそく！

( a + b ) × c

↓↓↓↓↓↓

( 1 + 2 ) × 3

= 3 × 3

= 9



( a + b ) × c に代入したときの計算結果は

9になりました。



もう片方についても考えます。



a × c + b × c

↓↓↓↓↓↓↓

1 × 3 + 2 × 3

= 3 + 6

= 9



両方とも計算結果が９になりましたね。

これで公式は問題なさそうです！！

そう思ったあなた！


とても素晴らしい考えです♪

ぜひあなた自身の手で他の数字についても

試してみてください。

分配法則を使う問題とは

分配法則は

かけ算とかっこ『（）』が使われている計算で

よく使われます！



問題文が『次の計算をしなさい』

という文章で

かけ算とかっこ『（）』が

となりあっていたら、

まず分配法則が関係するでしょう。



実際に使われている計算例は

例題で確認していきますね。

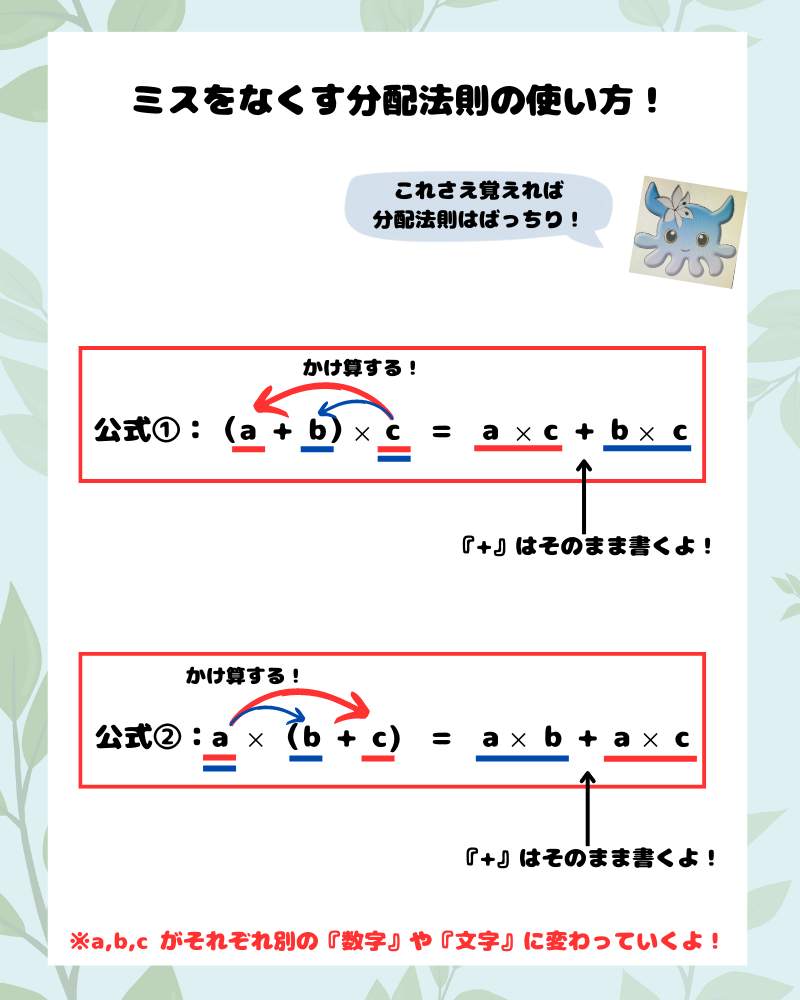
ミスをなくす分配法則の公式の使い方！

分配法則の公式のついてお話をしましたが、

実際計算するときに

『ミスをなくす分配法則の使い方』を紹介します。



ぜひ問題の度にこの図の内容を書いて

覚えていってください。

分配法則の練習問題を解いて苦手をなくそう！

ここからは例題を通して

計算に慣れていきます。



第２章ではプラスだけの計算

第３章ではマイナスが入った計算

という内容で進めていきます。



『ミスをなくす分配法則の使い方』



さえ覚えていれば

解けるように説明するので

あなたも一緒に解いてみてくださいね♪

例題１

例題１：次の計算をしなさい

（１）　( a + 2b ) × 5

（２）　( 6a + b ) × 2

（３）　3 ( 2 + 5a )

（４）　4 ( 3a + 2 )



例題として４問出しました。

この問題が解けるかどうか

計算してみてください。



うまく計算できなかったら

そのまま『簡単な解き方』に

進んでくださいね。



「解けたよ！」

という場合は

『例題１の答え』に進んでください。



答えが間違えていた場合は、

『簡単な解き方』を見ながら

真似して解いてみてくださいね。

簡単な解き方

（１）の問題から順番よく

簡単な解き方を紹介します。



画像で登場する『あなたのノート』の

とおり書いていけば答えにたどり着きますよ。




その前に！




問題を解くときのポイントを紹介します。

【ポイント！！】

問題を解くたびに

『ミスをなくす分配法則の使い方』を

書いてくださいね！

問題の度に書くことで

すぐに覚えることができますよ。

例題１　（１）

それでは解き方を説明していきます。

まず初めに（１）の問題を書き

その下に『ミスをなくす分配法則の使い方』を

書きます。

ここで、この問題が

公式のどちらを使うか

考えます。



（１）の場合は、

数字がかっこ『（）』の右側にあるので

公式①を使います。

公式①　( a + b ) × c

（１）　( a + 2b ) × 5

両方ともかっこ『（）』の右側に
かけ算の記号『×』があるね！

次に公式に書かれている

a,b,c が

問題では別の数字や文字に
なっているので

どう変化しているかを

確認します。

公式①　( a + b ) × c

（１）　( a + 2b ) × 5

公式と問題を見比べよう！

問題と公式を見比べることで



a のところには a

b のところには 2b

c のところには 5 がある。

ということが分かりました。

問題と公式を見比べることで

a → a

b → 2b

c → 5

とそれぞれ代入してあげることが

わかります。
（今回は a がそのままだね。）



a,b,c に代入する数字や文字が分かったので

実際に代入して計算をしていきましょう。

そうすれば答えにたどり着けます！

計算の結果

答え：5a + 10b

となることが分かりました。



１問解いてみたがどうだったでしょうか。

画像にある『あなたのノート』のように

計算を進めていくことで解くことができます。

公式にある『a , b , c』の代わりに


『a , 2b , 5』を入れてあげること

これを意識するだけでも

答えにたどり着くことができちゃうんです！



引き続き（２）～（４）も解いて

解き方を身に付けていきましょう。

ぜひ『あなたのノート』を参考に

進めてくださいね♪

例題１　（２）

それでは

（２） ( 6a + b ) × 2

を計算をしていきましょう。

まず初めに、

問題と『ミスをなくす分配法則の使い方』を

書いていきます。

問題が出る度に

『ミスをなくす分配法則の使い方』を書くことで

すぐに覚えられますよ！

次に公式のどちらを使うのか

確認します。

この問題も

（２）の場合も、

数字がかっこ『（）』の右側にあるので

公式①を使います。

公式①　( a + b ) × c

（２）　( 6a + b ) × 2

両方ともかっこ『（）』の右側に
かけ算の記号『×』があるね！

次に公式に書かれている

a,b,c が

問題では別の数字や文字に
なっているので

どう変化しているかを

確認します。

公式①　( a + b ) × c

（２）　( 6a + b ) × 2

公式と問題を見比べよう！

問題と公式を見比べることで

a のところには 6a

b のところには b

c のところには 2 がある。

ということが分かりました。

問題と公式を見比べることで

a → 6a

b → b

c → 2

とそれぞれ代入してあげることが

わかります。
（今回は b がそのままだね！）



a,b,c に代入する数字や文字が分かったので

実際に代入して計算をしていきましょう。

そうすれば答えにたどり着けます！

計算の結果

答え：12a + 2b

となることが分かりました。

公式にある『a , b , c』の代わりに

『6a , b , 2』を入れてあげること

これを意識しましょう。

例題１　（３）

続いて

（３） 3 ( 2 + 5a )

を解いていきます。



ここでもまず初めに

問題と『ミスをなくす分配法則の使い方』を

書いていきます。

さて、問題と公式を見比べて

どちらの公式を使うか確認しましょう。



これは数字がかっこ『（）』の左側にあるので

公式②を使いそう…。

っと、あれれ？

と思ったあなた！



ちょーないす♪♪



実は、

数字のすぐ右側のかけ算の記号『×』は

見えないように隠れてしまうということが
あるのです！！



ここで違いに気づけたのならとても素晴らしい♪

ぜひ覚えていてくださいね。

3 × ( 2 + 5a ) の場合

↓↓↓

3 ( 2 + 5a ) のように

かけ算のマーク『×』が隠れることがあります！！

この『×』が隠れていることを意識して、

書き直してあげると

公式②と同じ形になります。

隠れてた『×』を加えることで

公式②　a × ( b + c )

（３）　3 × ( 2 + 5a )

両方ともかっこ『（）』の左側に
かけ算の記号『×』があるね！

公式②を使うことが分かったので、

次に



a,b,c が

問題では別の数字や文字に
なっているので

どう変化しているかを

確認します。

公式②　a × ( b + c )

（３）　3 × ( 2 + 5a )

公式と問題を見比べよう！

式を見比べることで

a のところには 3

b のところには 2

c のところには 5a がある！

ということが分かります。

問題と公式を見比べることで

a → 3

b → 2

c → 5a

とそれぞれ代入してあげることが

わかります。




a,b,c に代入する数字や文字が分かったので

実際に代入して計算をしていきましょう。

そうすれば答えにたどり着けます！

計算の結果

答え：6 + 15a

となることが分かりました。

隠れた『×』を書き足すこと、

そして

公式にある『a , b , c』の代わりに

『3 , 2 , 5a』を入れてあげること

これを意識しましょう！！

例題１　（４）

いよいよ例題１（４）です！

（４） 4 ( 3a + 2 )

を解いていきます。



ここでもまず初めに

問題と『ミスをなくす分配法則の使い方』を

書いていきます。

さて、問題と公式を見比べて

どちらの公式を使うか確認しましょう。



これは数字がかっこ『（）』の左側にあるので

公式②を使いそう…。



でも、



『×』が見当たりませんね。

これも『×』が隠れているのです。

この『×』を書き足しましょう！！

隠れてた『×』を加えることで

公式②　a × ( b + c )

（４）　4 × ( 3a + 2 )

両方ともかっこ『（）』の左側に
かけ算の記号『×』があるね！

公式②を使うことが分かったので、

次に



a,b,c が

問題では別の数字や文字に
なっているので

どう変化しているかを

確認します。

公式②　a × ( b + c )

（４）　4 × ( 3a + 2 )

公式と問題を見比べよう！

式を見比べることで

a のところには 4

b のところには 3a

c のところには 2 がある。

ということが分かります。

問題と公式を見比べることで

a → 4

b → 3a

c → 2

とそれぞれ代入してあげることが

わかります。




a,b,c に代入する数字や文字が分かったので

実際に代入して計算をしていきましょう。

そうすれば答えにたどり着けます！

隠れた『×』を書き足すこと、

そして

公式にある『a , b , c』の代わりに

『4 , 3a , 2』を入れてあげること

これを意識しましょう！！

いかがだったでしょうか。

『ミスをなくす分配法則の使い方』を
覚えることはできましたか？



この形を覚えておくだけで

今までより問題が簡単に解けるようになること

間違いなしです！！

例題１の答え

例題１の問題とその答えを並べておきますので

改めて答えがあっているか確認してみてください。

例題１の場所に戻りたい場合は『こちら』から。

（１）　( a + 2b ) × 5　＝　5a + 10b

（２）　( 6a + b ) × 2　＝　12a + 2b

（３）　3 ( 2 + 5a )　＝　6 + 15a

（４）　4 ( 3a + 2 )　＝　12a + 8

（１）～（４）の

『あなたのノート』完成版も
まとめておいておきますので

ぜひ確認してみてください♪

マイナスが入ってきても大丈夫！ミスと苦手をなくそう！

次はいよいよ

マイナスが入った計算問題です！



ここでも『ミスをなくす分配法則の使い方』を
書いていくことで

問題が解けるように説明をしていきますので

安心して読み進めてくださいね！

例題２

例題２：次の計算をしなさい

（１） ( -5 + 3b ) × 5

（２） (3a – b ) × ( -4 )

（３） -2 ( -6 + 5a )

（４） -4 ( 3a – 2 )

ここでも例題を４問出してみました。



この問題が解けるかどうか

ぜひ１度計算してみてください。



うまく計算できなかったら

そのまま『簡単な解き方』に

進んでくださいね。



「解けたよ！」

という場合は

『例題２の答え』に進んでください。



答えが間違えていた場合は、

『簡単な解き方』を見ながら

真似して解いてみてくださいね。

マイナスがいる場合の簡単な解き方

ここでも（１）の問題から

順番よく

簡単な解き方を説明していきます。



『あなたのノート』の

手順通りに書いていくことで

答えにたどり着きますよ。



ここでひとつ！



マイナスが入る場合の
計算のポイントを紹介します。

ポイントは

かけ算をするときの符号の関係についてです。



かけ算をするとき、

プラス『＋』とプラス『＋』の
かけ算の答えはプラス『＋』
（＋と＋で＋）

プラス『＋』とマイナス『ー』の
かけ算の答えはマイナス『ー』
（＋とーでー）

マイナス『ー』とマイナス『ー』の
かけ算の答えはマイナス『ー』
（ーとーで＋）

となることを覚えていてください！

このかけ算のときの符号ミスで
点数を落としている生徒たちを
たくさん見てきました。



つまり！



ここを注意するだけで

点数が上がるということです！！！

同じ符号での計算なら『＋』

違う符号での計算なら『ー』


です。

それでは、

符号に注意しながら

（１）から解いていきましょう。

例題２　（１）

（１） ( -5 + 3b ) × 5

を解いていきます。



ここでもまず初めに

問題と『ミスをなくす分配法則の使い方』を

書いていきます。

慣れたからもういいや、
なんて思わず
必ず書くようにしましょう♪


ここで書くことで

あなたの点数が上がるのです♪

さて、

マイナスがいてもやることは変わりません。



問題と公式を見比べて

どちらの公式を使うか確認しましょう。




（１）の場合、

数字がかっこ『（）』の右側にあるので

公式①を使います。

公式①　( a + b ) × c

（１）　( -5 + 3b ) × 5

両方ともかっこ『（）』の右側に
かけ算の記号『×』があるね！

そして次に、

公式のa,b,c が

問題では別の数字や文字に
なっているので

どう変化しているかを

確認します。

公式①　( a + b ) × c

（１）　( -5 + 3b ) × 5

公式と問題を見比べよう！

問題と公式を見比べることで

a のところには -5

b のところには 3b

c のところには 5 がある。

ということが分かります。

問題と公式を見比べることで

a → -5

b → 3a

c → 5

とそれぞれ代入してあげることが

わかりました。




公式のa,b,c に代入する数字や文字が分かったので

実際に代入して計算をしていきましょう。

そうすれば答えにたどり着けます！

マイナス『ー』とプラス『＋』の
かけ算の場合は
違う符号どうしなのでマイナス『ー』になる！

そして

公式にある『a , b , c』の代わりに

『-5 , 3b , 5』を入れてあげること

これを意識しましょう！！

マイナスが出てきても心配することはありません。

『ミスをなくす分配法則の使い方』を使って

ゆっくり確実に計算していけばいいのです！！

例題２　（２）

続いて

（２） ( 3a – b ) × (-4)

この計算問題を解いていきましょう。


おや、ここでは

かけ算の記号『×』の右側にある数字

『-4』にもかっこ『（）』が付いていますね。



実は！



これは式の書き方の特徴のひとつなのです。

もしもこのかっこ『（）』がないと

（２） ( 3a – b ) × -4

となり、

かけ算の記号『×』と

マイナス『ー』が続いてしまいますね。



数学ではこのように

計算の記号がつながることを
避けたがります！

けっこう見づらくなるので…。



なので、



計算の記号どうしが並ぶときは

かっこ『（）』を間に使うことがあります。

これは計算の途中でも同じですので

これを機会に意識していきましょう。



それでは、



計算の記号の間にあるかっこ『（）』に
気を付けながら

問題と『ミスをなくす分配法則の使い方』を
書いていきましょう。

さて、

（１）と少し見た目がちがいますが、

やることは変わりません。



問題と公式を見比べて

どちらの公式を使うか確認しましょう。




（２）の場合も、

数字がかっこ『（）』の右側にあるので

公式①を使います。

公式①　( a + b ) × c

（１）　( 3a – b ) × ( -4 )

両方ともかっこ『（）』の右側に
かけ算の記号『×』があるね！

公式①を使うことが
わかったので、

公式のa,b,c が

問題では別の数字や文字に
なっているので

どう変化しているかを

確認します。

公式①　( a + b ) × c

（２）　( 3a – b ) × ( -4 )

公式と問題を見比べよう！

問題と公式を見比べることで

a のところには 3a

b のところには -b

c のところには ( -4 ) がある。

ということが分かります。

ここでは

公式①の『＋ｂ』が

『ーｂ』に変わっていることになります！

問題と公式を見比べることで

a → 3a

b → -b

c → ( -4 )

とそれぞれ代入してあげることが

わかりました。




公式のa,b,c に代入する数字や文字が分かったので

実際に代入して計算をしていきましょう。

そうすれば答えにたどり着けます！

マイナス『ー』とプラス『＋』の
かけ算の場合は
違う符号どうしなのでマイナス『ー』になる！

また、

マイナス『ー』とマイナス『ー』の
かけ算の場合は
同じ符号どうしなのでプラス『＋』になる！

そして

公式にある『a , b , c』の代わりに

『3a , -b , ( -4 )』を入れてあげること

これを意識しましょう！！

例題２　（３）

続いて

（３） -2 ( -6 + 5a )

この問題を計算していきます！

ここでもまず初めに

問題と『ミスをなくす分配法則の使い方』を

書いていきます。

おっと、

この問題、

かっこ『（）』の左側に
かけ算の記号『×』がありませんね。



ならば、



隠れている『×』に
出てきてもらいましょう！

隠れていた『×』が
出てきたことで

公式②と同じ形をしていることが
わかりますね♪

公式②　 a × ( b + c )

（３）　-2 × ( -6 + 5a )

両方ともかっこ『（）』の左側に
かけ算の記号『×』があるね！

公式①を使うことが
わかったので、

公式のa,b,c が

問題では別の数字や文字に
なっているので

どう変化しているかを

確認します。

公式①　 a × ( b + c )

（２）　-2 × ( -6 + 5a )

公式と問題を見比べよう！

問題と公式を見比べることで

a のところには -2

b のところには -6

c のところには 5a がある。

ということが分かります。

問題と公式を見比べることで

a → -2

b → -6

c → 5a

とそれぞれ代入してあげることが

わかりました。




公式のa,b,c に代入する数字や文字が分かったので

実際に代入して計算をしていきましょう。

そうすれば答えにたどり着けます！

マイナス『ー』とマイナス『ー』の
かけ算の場合は
同じ符号どうしなのでプラス『＋』になる！

また、

マイナス『ー』とプラス『＋』の
かけ算の場合は
ちがう符号どうしなのでマイナス『ー』になる！

そして

公式にある『a , b , c』の代わりに

『-2 , -6 , 5a』を入れてあげること

これを意識しましょう！！



計算の記号がくっつきそうな場合は

-2 × ( -6 )のように

かっこ『（）』を間に入れるのを
忘れずに。

例題２　（４）

最後の例題！

（４）　-4 ( 3a -2 )

この計算をやっていきます。


最後までちゃんと、

初めに

問題と『ミスをなくす分配法則の使い方』を

書いていきます。

あら、

この問題も、

かっこ『（）』の左側に
かけ算の記号『×』がありませんね。



それでは、



隠れている『×』に
出てきてもらいましょう。

んー、
っぽ！！

隠れていた『×』が
出てきたことで

公式②と同じ形をしていることが
わかりますね♪

公式②　 a × ( b + c )

（４）　-4 × ( 3a – 2 )

両方ともかっこ『（）』の左側に
かけ算の記号『×』があるね！

公式①を使うことが
わかったので、

公式のa,b,c が

問題では別の数字や文字に
なっているので

どう変化しているかを

確認します。

公式①　 a × ( b + c )

（２）　-4 × ( 3a – 2)

公式と問題を見比べよう。

問題と公式を見比べることで

a のところには -4

b のところには 3a

c のところには -2 がある。

ということが分かります。

ここでは

公式②の『 + c 』が

『 -2 』に変わっていることになります。

問題と公式を見比べることで

a → -4

b → 3a

c → -2

とそれぞれ代入してあげることが

わかりました。




公式のa,b,c に代入する数字や文字が分かったので

実際に代入して計算をしていきましょう。

そうすれば答えにたどり着けます。



さあ、



もうひといき♪

マイナス『ー』とプラス『＋』の
かけ算の場合は
ちがう符号どうしなのでマイナス『ー』になる！

また、

マイナス『ー』とマイナス『ー』の
かけ算の場合は
同じ符号どうしなのでプラス『＋』になる！

そして

公式にある『a , b , c』の代わりに

『-4 , 3a , -2』を入れてあげること

これを意識しましょう！！



計算の記号がくっつきそうな場合は

( -4 ) × ( -2 )のように

かっこ『（）』を間に入れるのを
忘れずに。

お疲れ様です♪

マイナスが入った分配法則の
計算をたくさんしてきましたが、

『ミスをなくす分配法則の使い方』を
覚えることはできましたか？


この形を覚えておくだけで

マイナスが入った計算問題でも
簡単に解けるようになること

間違いなしです。

ぜひこれを機械に
使いこなしてくださいね♪

例題２の答え

例題２の問題とその答えを並べておきますので

改めて答えがあっているか確認してみてください。

例題２の場所に戻りたい場合は『こちら』から。

（１）　( -5 + 3b ) × 5　＝　-25 + 15b


（２）　( 3a – b ) × ( -4 )　＝　-12a + 4b


（３）　-2 ( -6 + 5a )　＝　12 – 10a


（４）　-4 (3a – 2 )　＝　-12a + 8

（１）～（４）の

『あなたのノート』完成版も
まとめておいておきますので

ぜひ確認してみてください♪

さいごに　そして練習問題！！

お疲れさまでしたー☆彡

たくさんの分配法則を解きましたね。

ここまで読んでいただけて嬉しいです♪


『ミスをなくす分配法則の使い方』を
使えばミスが限りなく減ります。



『あなたのノート』完成版を見ながら
何度も解きなおしてくださいね。




大事なことは




『何度も復習すること！』
ですよ♪


もう覚えた、わかったと

油断していると
簡単なミスをしてしまいます。

それはとてももったいないので

簡単な計算ミスや符号ミスに
気を付けながら

これからも問題を
たくさん解いてくださいね♪



ここで
サービス問題！！


さらに追加で８問
プレゼントしちゃいます♪


答えも問題の下に用意してますので
あなた自身の力で解いてみてくださいね。

練習問題☆彡

（１）　( 2a + 6 ) × 9

（２）　( 3 + b ) × 7

（３）　6 ( 2a + 3b )

（４）　２( 6a + 9 )

（５）　( -7 + 4b ) × 5

（６）　( 3a – 8 ) × ( -10 )

（７）　-5 ( -2a + 8b )

（８）　-4 ( 7a – 5 )

練習問題の答え

（１）　( 2a + 6 ) × 9　＝　18a + 54

（２）　( 3 + b ) × 7　＝　21 + 7b

（３）　6 ( 2a + 3b )　＝　12a + 18b

（４）　２( 6a + 9 )　＝　12a + 18

（５）　( -7 + 4b ) × 5　＝　-35 + 20b

（６）　( 3a – 8 ) × ( -10 )　＝　-30a + 80

（７）　-5 ( -2a + 8b )　＝　10a – 40b

（８）　-4 ( 7a – 5 )　＝　-28a + 20

さいごに

この記事を見つけていただき、

また、読んでいただきありがとうございました。

この記事について、



何か気になること



もっと教えてほしいこと



聞きたいことがございましたら

コメント
またはTwitter（@Mendakoyuri)まで
ご連絡ください！！

この記事の他にも


【苦手でも問題の解き方が分かる！】中学校 数学：０より小さい数

【苦手でも解ける！】中学数学②：「30kg重い」は「-30kg軽い」と同じ！？

【苦手でも解ける！】中学数学の絶対値って何！！！
（※↑それぞれ、クリックすると別のページが開きます）

といった

中学数学に関する記事を紹介しております。


ぜひ受験や日々の勉強に役立ててください♪♪


以上
めんだこてぃすブログでした☆彡